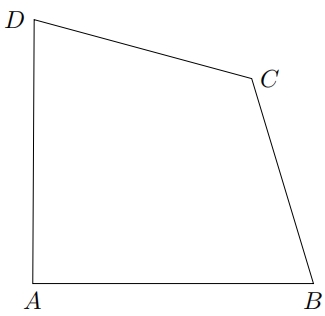
如图,给定一个任意四边形$ ABCD $,边长和角度都是未知的 如何作一条直线,将该四边形分为面积相等的2个部分? 步骤如下:
-
连接对角线$ BD $,过$ C $点作一条直线$ l $,使得$ l // BD $,且$ l $与$ AB $的延长线相交于点$ E $
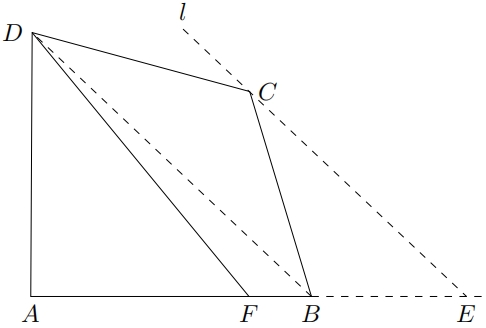
-
取线段$ AE $的中点$ F $,连接$ DF $,$ DF $将该四边形分为面积相等的2个图形
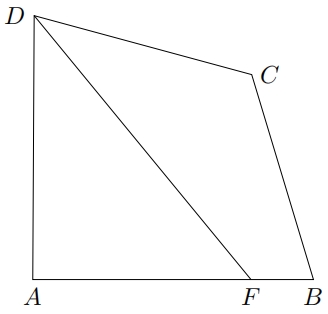
要如何证明$ \triangle AFD $与四边形$ BCDF $面积相等? 连接$ DE $,$ DE $与$ BC $相交于点$ O $
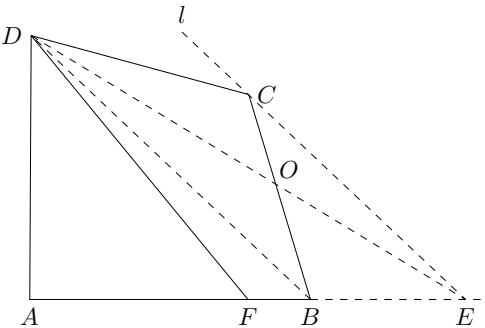
由$ l // BD $可知,$ S_{\triangle BCD}=S_{\triangle BDE} $ $ \triangle BOD $为$ \triangle BCD $与$ \triangle BDE $的公共部分,由此可得出
$$ \large \begin{align*} S_{\triangle OCD}=S_{\triangle OBE}\newline S_{\text{四边形}ABCD}=S_{\triangle ADE} \end{align*} $$点$ F $为线段$ AE $中点,由此可知
$$ \large S_{\triangle AFD}=S_{\triangle EFD}=S_{\text{四边形}BCDF} $$证毕!
