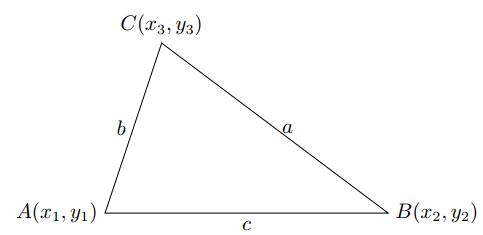
已知平面直角坐标系内,$ \triangle ABC $三点坐标$ A(x_{1},y_{1}),B(x_{2},y_{2}),C(x_{3},y_{3}) $,边长$ AB=c,BC=a,AC=b $
重心
点$ O(x,y) $为$ \triangle ABC $的重心,则有
$$ \large \begin{align*} & \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\\[2mm] &\left\{\begin{array}{l} x=\dfrac{1}{3}(x_{1}+x_{2}+x_{3})\\[6mm] y=\dfrac{1}{3}(y_{1}+y_{2}+y_{3}) \end{array}\right. \end{align*} $$内心
点$ O(x,y) $为$ \triangle ABC $的内心,则有
$$ \large \begin{align*} & a \cdot \overrightarrow{OA}+b \cdot \overrightarrow{OB}+c \cdot \overrightarrow{OC}=\overrightarrow{0}\\[2mm] & \left\{\begin{array}{l} x=\dfrac{x_{1}\sin A+x_{2}\sin B+x_{3}\sin C}{\sin A+\sin B+\sin C}\\[6mm] y=\dfrac{y_{1}\sin A+y_{2}\sin B+y_{3}\sin C}{\sin A+\sin B+\sin C} \end{array}\right. \end{align*} $$外心
点$ O(x,y) $为$ \triangle ABC $的外心,则有
$$ \large \begin{align*} & \sin 2A \cdot \overrightarrow{OA}+\sin 2B \cdot \overrightarrow{OB}+\sin 2C \cdot \overrightarrow{OC}=\overrightarrow{0}\\[2mm] & \left\{\begin{array}{ll} x &=\dfrac{x_{1}\sin 2A+x_{2}\sin 2B+x_{3}\sin 2C}{\sin 2A+\sin 2B+\sin 2C}\\[6mm] &=\dfrac{x_{1}\sin 2A+x_{2}\sin 2B+x_{3}\sin 2C}{4\sin A\sin B\sin C}\\[6mm] y &=\dfrac{y_{1}\sin 2A+y_{2}\sin 2B+y_{3}\sin 2C}{\sin 2A+\sin 2B+\sin 2C}\\[6mm] &=\dfrac{y_{1}\sin 2A+y_{2}\sin 2B+y_{3}\sin 2C}{4\sin A\sin B\sin C} \end{array}\right. \end{align*} $$垂心
点$ O(x,y) $为$ \triangle ABC $的垂心,则有
$$ \large \begin{align*} & \sin A\cos B\cos C \cdot \overrightarrow{OA}+\sin B\cos A\cos C \cdot \overrightarrow{OB}+\sin C\cos A\cos B \cdot \overrightarrow{OC}=\overrightarrow{0}\\[2mm] & \left\{\begin{array}{ll} x & =\dfrac{x_{1}\sin A\cos B\cos C+x_{2}\sin B\cos A\cos C+x_{3}\sin C\cos A\cos B}{\sin A\cos B\cos C+\sin B\cos A\cos C+\sin C\cos A\cos B}\\[6mm] & =\dfrac{x_{1}\sin A\cos B\cos C+x_{2}\sin B\cos A\cos C+x_{3}\sin C\cos A\cos B}{\sin A\sin B\sin C}\\[6mm] y & =\dfrac{y_{1}\sin A\cos B\cos C+y_{2}\sin B\cos A\cos C+y_{3}\sin C\cos A\cos B}{\sin A\cos B\cos C+\sin B\cos A\cos C+\sin C\cos A\cos B}\\[6mm] & =\dfrac{y_{1}\sin A\cos B\cos C+y_{2}\sin B\cos A\cos C+y_{3}\sin C\cos A\cos B}{\sin A\sin B\sin C} \end{array}\right. \end{align*} $$旁心
1、点$ O(x,y) $为$ \angle A $所对的旁心,则有
$$ \large \begin{align*} & a \cdot \overrightarrow{OA}-b \cdot \overrightarrow{OB}-c \cdot \overrightarrow{OC}=\overrightarrow{0}\\[2mm] & \left\{\begin{array}{l} x=\dfrac{x_{1}\sin A-x_{2}\sin B-x_{3}\sin C}{\sin A-\sin B-\sin C}\\[6mm] y=\dfrac{y_{1}\sin A-y_{2}\sin B-y_{3}\sin C}{\sin A-\sin B-\sin C} \end{array}\right. \end{align*} $$2、点$ O(x,y) $为$ \angle B $所对的旁心,则有
$$ \large \begin{align*} & b \cdot \overrightarrow{OB}-a \cdot \overrightarrow{OA}-c \cdot \overrightarrow{OC}=\overrightarrow{0}\\[2mm] & \left\{\begin{array}{l} x=\dfrac{x_{2}\sin B-x_{1}\sin A-x_{3}\sin C}{\sin B-\sin A-\sin C}\\[6mm] y=\dfrac{y_{2}\sin B-y_{1}\sin A-y_{3}\sin C}{\sin B-\sin A-\sin C} \end{array}\right. \end{align*} $$3、点$ O(x,y) $为$ \angle C $所对的旁心,则有
$$ \large \begin{align*} & c \cdot \overrightarrow{OC}-b \cdot \overrightarrow{OB}-a \cdot \overrightarrow{OA}=\overrightarrow{0}\\[2mm] & \left\{\begin{array}{l} x=\dfrac{x_{3}\sin C-x_{2}\sin B-x_{1}\sin A}{\sin C-\sin B-\sin A}\\[6mm] y=\dfrac{y_{3}\sin C-y_{2}\sin B-y_{1}\sin A}{\sin C-\sin B-\sin A} \end{array}\right. \end{align*} $$