在上一篇文章👉 《一元四次方程的解法:费拉里法》 中,我们介绍了如何用费拉里法解一元四次方程。本文将介绍更多的解法
笛卡尔-欧拉解法
对于一元四次方程
$$ \large y^4+ay^3+cy^2+dy+e=0 $$令$ y=x-\dfrac{a}{4} $,代入化简得
$$ \large x^4+px^2+qx+r=0 $$设$ z_1,z_2,z_3 $是方程
$$ \large z^3+\frac{p}{2}z^2+\frac{p^2-4r}{16}z-\frac{q^2}{64}=0 $$的三个根,则$x^4+px^2+qx+r=0$的四个根$ x_1,x_2,x_3,x_4 $是
$$ \large \pm \sqrt{z_1}\pm \sqrt{z_2}\pm \sqrt{z_3} $$式中符号的选取应满足
$$ \large \sqrt{z_1} \cdot \sqrt{z_2} \cdot \sqrt{z_3}=-\frac{q}{8} $$退化解法
退化解法来源于解析几何中二次曲线退化的判别条件。 设$ ax^4+bx^3+cx^2+dx+e=0\quad (a \neq 0) $是一个一元四次方程,引进参数$ t $,使之满足三次方程
$$ \large \begin{vmatrix} 2a & b & t\\[2mm] b & 2(c-t) & d\\[2mm] t & d & 2e \end{vmatrix}=0 $$即$ t^3-ct^2+(bd-4ae)t+(4ace-ad^2-eb^2)=0 $,设$ t_0 $为它的任一个根,代入原方程,则方程
$$ \large ax^4+bx^3+(c-t_0)x^2+t_0x^2+dx+e=0 $$可分解为两个二次方程。解之,即得原方程的四个根。 在解析几何中,二次曲线$ ax^2+bxy+cy^2+dx+ey+f=0(a\neq 0) $退化的充分必要条件是
$$ \large \Delta= \begin{vmatrix} 2a & b & d\\[2mm] b & 2c & e\\[2mm] d & e & 2f \end{vmatrix}=0 $$如果令$ x=y^2 $,相应地有
$$ \large ay^4+by^3+(ced)y^2+ey+f=0 \quad (a \neq 0) $$退化的充分必要条件是$ \Delta=0 $。因此,上述的解四次方程的方法称为退化解法
解整系数四次方程的*法
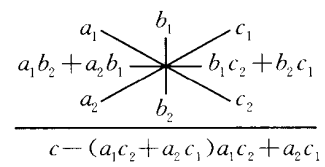
该法是十字相乘法的推广,可用于整系数四次多项式分解成两个整系数二次多项式之积。 设$ p(x)=ax^4+bx^3+cx^2+dx+e $是一个整系数多项式,且能分解成两个整系数多项式$ (a_1x^2+b_1x+c_1) $与$ (a_2x^2+b_2x+c_2) $的乘积,则$ a=a_1a_2,e=c_1c_2 $,即$ a_1,a_2 $可在$ a $的因子中寻找,$ c_1,c_2 $可在$ e $的因子中寻找 乘积中二次项的系数为$ a_1c_2+a_2c_1+b_1b_2 $,因此$ b_1b_2=c-(a_1c_2+a_2c_1) $,故$ b_1,b_2 $可在$ c-(a_1c_2+a_2c_1) $的因子中寻找。如果能够找到适当的$ b_1,b_2 $,使$ a_1b_2+a_2b_1=b,b_1c_2+b_2c_1=d $,则问题就全部解决了,否则换其他的$ b_1,b_2 $再试,如果各种可能的$ b_1,b_2 $都不行,就须改变$ a_1,a_2,c_1,c_2 $的组合或数值再试
