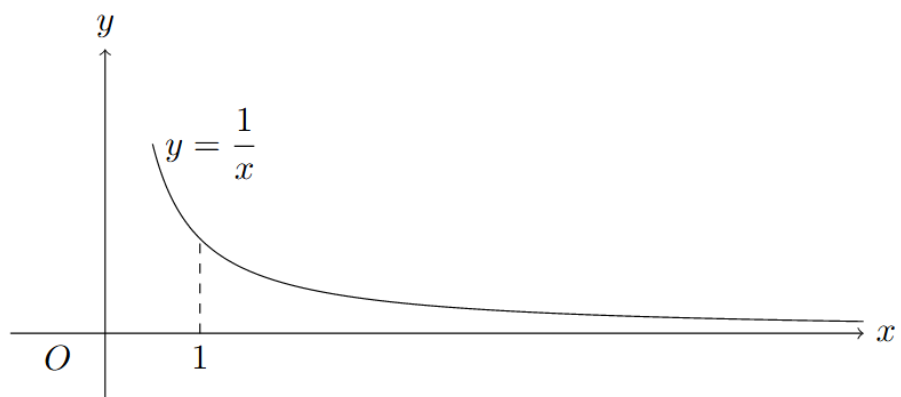
如下图,因其形状类似乐器小号,因此该物体被称为托里拆利小号,又称加百利号角
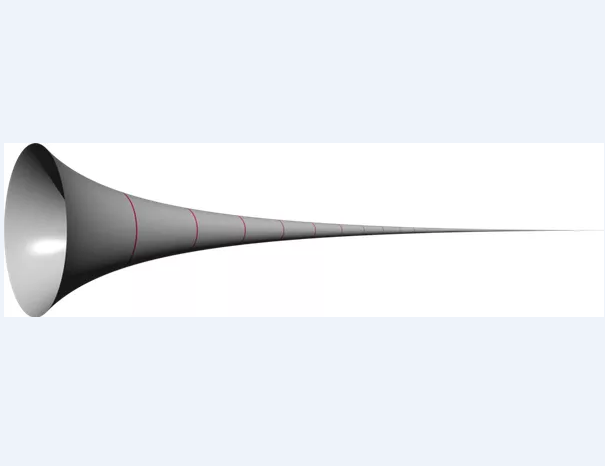
该物体的体积
$$ \large \begin{align*} V &= \pi\int_{1}^{+\infty}y^{2}\mathrm{d}x\\[4mm] &= \pi\int_{1}^{+\infty}\frac{1}{x^{2}}\mathrm{d}x\\[4mm] &=-\frac{\pi}{x}\bigg|_{1}^{+\infty}\\ &=\pi \end{align*} $$表面积
$$ \large \begin{align*} S &=2\pi\int_{1}^{+\infty}y\sqrt{1+(y')^{2}}\mathrm{d}x\\[4mm] &=2\pi\int_{1}^{+\infty}\frac{1}{x}\sqrt{1+\frac{1}{x^{4}}}\mathrm{d}x\\[4mm] & \geqslant 2\pi\int_{1}^{+\infty}\frac{1}{x}\mathrm{d}x\\[4mm] \end{align*} $$广义积分$ \displaystyle 2\pi\int_{1}^{+\infty}\frac{1}{x}\mathrm{d}x=+\infty $,发散,因此表面积无限